 In the March 2020 issue of The Compendium (Vol. 27-1) from NASS I discussed how to make a simple triangle gnomon. We'll extend this tutorial to add a rounded tip and then examine how to make a gnomon with an underneath cut-back for a more pleasing shape.
In the March 2020 issue of The Compendium (Vol. 27-1) from NASS I discussed how to make a simple triangle gnomon. We'll extend this tutorial to add a rounded tip and then examine how to make a gnomon with an underneath cut-back for a more pleasing shape.
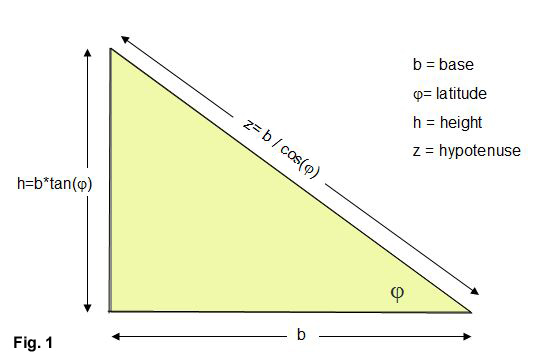
The fundamental triangle has a base b, height h, and hypotenuse z. To make the triangle proportions for the sundial latitude \(\phi\), we observe that the hypotenuse must point to the north (or south) celestial pole. As shown in (Fig. 1) :
We'll start out making the gnomon in a self-contained OpenSCAD module that at first simply creates the gnomon in the x-y plane. Here's the code:
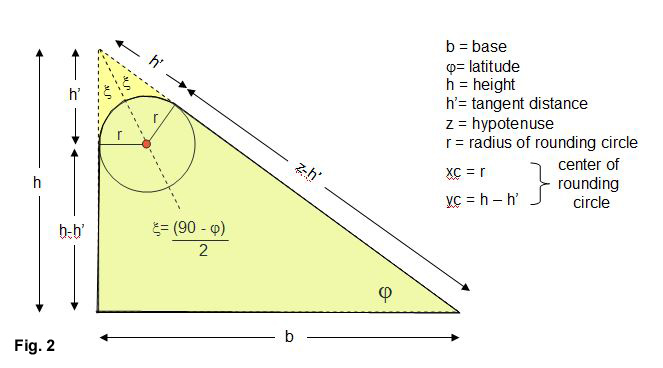
In the full code, we'll rotate and translate the gnomon so that it sits on top of the sundial we've designed inthe previous tutorials. But first, let's improve the gnomon with a rounded tip. From Fig. 2 we see that the rounding circle is centered on a bisected line from the apex and is tangent to both triangle's vertical and hypotenuse sides. We've labeled the tangent distance from the apex as h' on these sides. If we specify the rounding circle's radius r we see that the apex triangle half-angle \(\xi\) can be derived from the sum of angles equal to 180 degrees. Rearranging we get:
\( h' = \frac{r}{tan\xi} \)
The x-y tangent coordinate on the vertical side of the triangle is [0,h-h']. The x-y tangent coordinate on the hypotenuse is a bit more complicated, giving [b - (z-h')* cos\(\phi\), (z-h')*sin\(\phi\)]. These points help create a 4-point polygon to which we add the rounding cylinder:
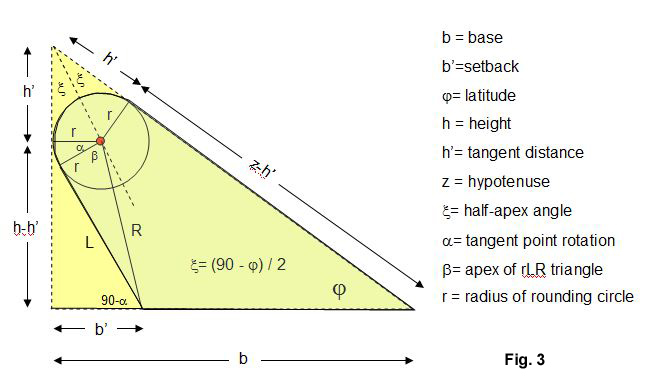 Now let's go even further by using a setback of the base where we move the vertical portion of the triangle back underneath the hypotenuse. The setback rotates the exact point of tangency with the rounding circle, so that we need a little more trignometry. In Fig. 3 the new gnomon setback line is L. To determine L we use the circle center to setback distance R as well as determining the apex angles alpha and beta:
Now let's go even further by using a setback of the base where we move the vertical portion of the triangle back underneath the hypotenuse. The setback rotates the exact point of tangency with the rounding circle, so that we need a little more trignometry. In Fig. 3 the new gnomon setback line is L. To determine L we use the circle center to setback distance R as well as determining the apex angles alpha and beta:
\( R=\sqrt{(b'-r)^2+(h-h')^2}\)
The length R and rounding circle radius give the apex angle \(\beta\):
All that remains is finding \(\alpha\). We see that the side L is actually part of two triangles. One is the rLR triangle with apex angle \(\beta\) and the other triangle is made from the setback b' and angle 90-\(\alpha\). Two equations can be formed which after some algebra reduces to:
 \(\frac{ (b'-r) - r*cos\alpha} {L} = -sin\alpha\)
\(\frac{ (b'-r) - r*cos\alpha} {L} = -sin\alpha\)Adding them together and rearranging
\(cos\alpha = \frac{r*(r-b') + L*(h-h') } {r^2 + L^2 }\)
With \(\alpha\) the indented tangent point is easily found as
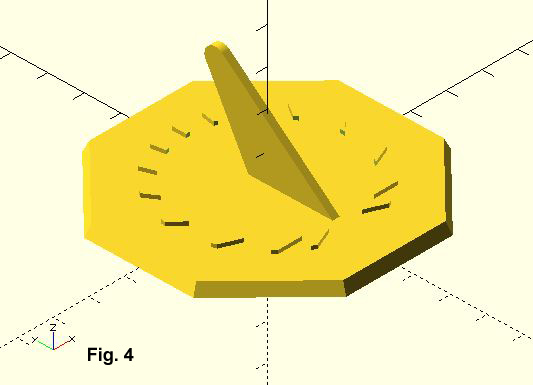
Pick up the attached OpenSCAD tutorial file and see the full code to attach either the simple, rounded, or setback gnomon onto you dial. In the next tutorial, we'll add hour numbers to the dial.