- Details
- Hits: 10448
By Robert L. Kellogg, Ph. D.
Benjamin Banneker, 1731-1806 , is one of the nation's best-known African American inventors. He was born in Maryland and in 1791 played an important part in surveying the newly designed Federal Territory, now called the District of Columbia. In his youth, Banneker was inspired to build his own clock after an acquaintance gave him a watch. He took the watch apart to find out how it worked and made drawings of each component, and based on his drawings, he carved larger versions of the components out of wood and constructed a clock that kept accurate time for more than 50 years. As mathematician, he designed an Almanac that was a rival of Benjamin Franklin’s famous publication.
As astronomer, clockmaker, and mathematician, he was expected to know how to design sundials, although none exist bearing his mark. In an age before pocket calculators, how would Banneker design a sundial? The graphical method is available in modern texts such as Waugh’s 1973 classic “Sundials: Theory and Construction”. Want to lay out a horizontal sundial without sines, cosines, and tangents? Then this “Sundials for Starters” is for you.
 Banneker-Dial Construction.pdf | [ ] | 2019 kB |
- Details
- Hits: 13533
One of the more interesting news items over the last several months has been the “Manhattan Henge” craze. Neil deGrasse Tyson, director of the Hayden Planetarium in New York, calculated the alignment of the sundown the street corridors of Manhattan (Fig. 1). For New Yorkers, two opportunities for alignment occur. The streets are aligned 28.9o east from North, and the sun sets near this at this azimuth on May 30-31 and July 11-12.
These alignments are just a small part of “shadow planes” where the shadow of the sun aligns with a building wall or other object. The best description of shadow planes comes from the NASS expert, Mac Oglesby and his compatriots William Maddux and Fer deVries in a series of three articles in The Compendium.[1]
- Details
- Hits: 20027
This Sundials for Starters appeared in The Compendium in December, 2005
by Robert Kellogg, Ph.D.
This is the start of a regular column to review the basics of Sundials. Of course NASS provides an introductory CD disk on sundials and there is always the classic reference Sundials, Their Theory and Construction by A.E. Waugh.
For this article, let’s consider some basics in buying a sundial for the garden. Or perhpas you want to make one. There are magazine catalogs and websites that offer “fine English dials”. But are they for you? Consider the latitude of an English dial. London is at about 51º north latitude, while most of the populated area of North America is below 45º. Take a look at the gnomon of your potential purchase. The gnomon should be approximately the same angle as you latitude. Here we’ll illustrate a dial (Figure 1) from the Naval Medical Center in Bethesda, Maryland with latitude of approximately 38º.
 SerlesRuler.jpg | [ ] | 37 kB |
- Details
- Hits: 14245
This Sundials for Starters appeared in The Compendium in March, 2006
by Robert L. Kellogg, Ph.D
I usually get up at 7am (ante meridian), but unlike ancient farmers, the time of rise has almost nothing to do with sunrise. One June 21st, and just west of Washington D.C. my sunrise occurs at 5:43 am Eastern Daylight Time (EDT). That would be 4:43 am Eastern Standard Time (EST) if we left our clocks alone. I’m almost due west of Washington D.C. and the Ellipse in front of the White House. Interesting, my sunrise will occur about 44 seconds after sunlight rises on the White House. How does this relate to longitude?
- Details
- Hits: 30777
This Sundials for Starters appeared in The Compendium in December 2013
Robert L. Kellogg, Ph.D.
|
Fig. 1 Analemma over the Acropolis photographed during the year by Ayiomamitis |
As the shadows grow longer and we head for the winter solstice my mind turns again to the analemma, a concept invented by Grandjean de Fouchy in 1740 to describe the apparent irregular motion of the sun. Strictly speaking, this is the difference between the right ascension of the true sun minus the right ascension of the mean sun. While this is mathematically important to astronomers, it is esthetically pleasing that the apparent sun will describe a “figure 8” through annual motion in the sky. This “figure 8” or analemma is visible only when the sun’s position is compared to a “mean time” using a precise clock. The analemma (or the sun’s apparent East-West motion called the Equation of Time) allows us to answer the question “Will the time shown on my sundial be fast or slow compared with my watch?”
- Details
- Hits: 18116
This Sundials for Starters appeared in The Comendium in June 2010
by Robert Kellogg, Ph.D.
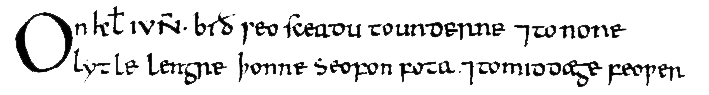Some years ago I had the thrill of reading the Tiberius manuscript1, which in Old English presented a horologium, a set of shadow lengths, from somewhere in England. The shadow lengths were given throughout the year, such as on Christ’s Mass day where “the shadow at [mid] morning and nine [halfway through the afternoon] is twenty [less] a heel foot and at midday four and twenty.”
1 MS Cotton Tiberius A, iii – folio 179 o/v British Museum, Manuscript Library