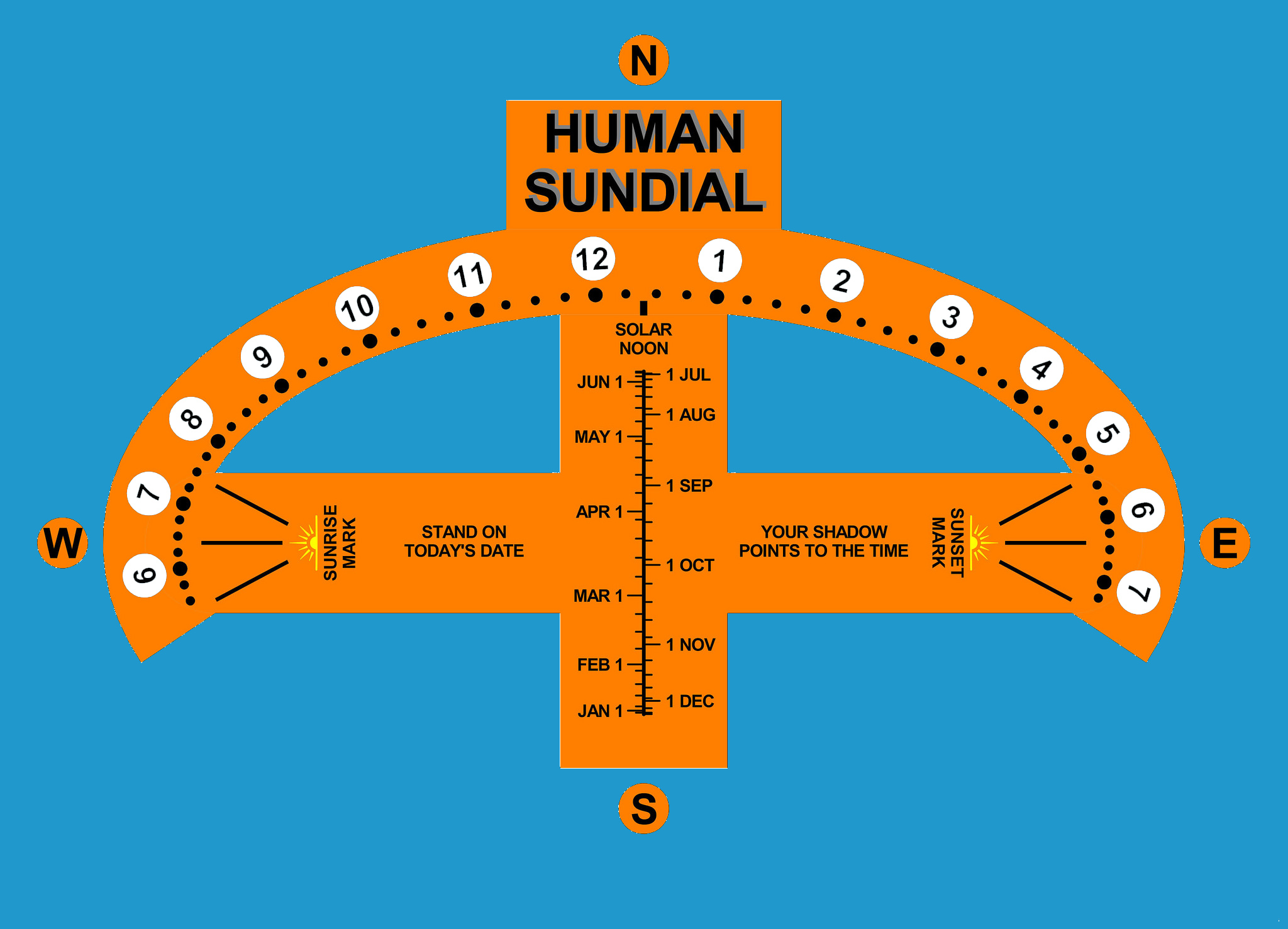
 The analemmatic sundial is unique with the ability to use a gnomon (the shadow casting element) of any height. This leads to the popular use of the analemmatic sundial as a "human sundial" where people use their own shadow to tell time.
The analemmatic sundial is unique with the ability to use a gnomon (the shadow casting element) of any height. This leads to the popular use of the analemmatic sundial as a "human sundial" where people use their own shadow to tell time.
Unlike garden horizontal dials or vertical dials on buildings, the analemmatic sundial requires a moveable gnomon. The position of the gnomon or where the person stands must be changed depending upon the season. A central walkway or guide indicates that a person should stand closer to the sun's noon hour mark at summer solstice and in reverse, stand much further south for the winter solstice. At the equinoxes the gnomon or person stands on a east-west line connecting the solar hours of 6am and 6pm.
Time on the analemmatic sundial is usually read simply with hour marks made on an ellipse. We recommend an ellipse with semi-major axis (the distance from the center of the walkway to the 6am or to the 6pm solar mark) of 6 to 8 feet (2 to 2.5 meters). The semi-minor axis and date marks on the walkway depend upon the sundial's latitude.
Using the symbol \(\phi\) for the sundial latitude and \(M\) for the sundial's semi-major axis, the semi-minor axis \(m\) is given by the simple equation:\[ \begin{equation} m = M \sin(\phi) \end{equation} \]
The semi-major axis is oriented exactly east-west and the semi-minor axis is aligned exactly north-south. We'll call the point where they cross the origin. At the sundial site our first task is to draw out these two perpendicular lines ensuring their east-west (x-axis) and north-south (y-axis) are correctly oriented. Next we need to draw this ellipse. Here we take advantage of the fact that the distance from one ellipse focus to the ellipse line and back to the other focus is constant everywhere around the ellipse, and this constant distance equals twice the semi-major axis. Therefore we need to find the distance of the focal points along the east-west line (x-axis). Their are two focal points: \[ \begin{equation} F_1 = -\sqrt{M^2 - m^2} \quad \text{ and } \quad F_2 = +\sqrt{M^2 - m^2}\end{equation}\].
For example, if M = 6 feet at latitude 40° N, m = 3.86 feet (3ft 10in) giving \(F = \pm 4.6 \text{ ft}\).

In practice we can draw the ellipse by making a length of string going from one focus \(F_1\) to the solar noon point (semi-minor axis) to the other focus \(F_2\). Then holding the string firm at the two foci, use a piece of chalk pulling the string taught. As you move the chalk while keeping the string taught, you will trace out the sundial's ellipse.
Once you have the ellipse, the hours can be easily marked. Let H be the angle of the sun away from solar noon. We call this the hour angle. Remember that there are 15 degrees per hour, so for example if the time is 10am, this is 2 hours before noon or H = -30°. Likewise 3pm is 3 hours after noon or H = 45°. We compute the hour mark on the ellipse from 6am (-90°) to 6pm (+90°). The x (east-west) and y (north-south) distances from the origin are:
\[ \begin{equation} x = M \sin(H)\end{equation}\] and \[ \begin{equation} y = M\sin(\phi)\sin(H)\end{equation}\]
The walkway is a bit more complicated since it depends upon the distance the sun from the celestial equator. The sun follows the annual path of 23.4° south of the equator at the winter solstices to 23.4° north of the equator at the summer solstices. This angle is called the sun's declination, noted by the symbol \(\delta\). At both the spring and fall equinox the sun is on the celestial equator at 0° declination. Let's call Z the distance from the origin up or down the y-axis that represents the place where we should stand:
\[ \begin{equation} Z = M\tan(\delta)\cos(\phi)\end{equation} \]

| Date | Declination | Date | Declination | |
| Jan 1 | -23.1° | July 1 | 22.0° | |
| Feb 1 | -17.3° | Aug 1 | 18.2° | |
| Mar 1 | -7.9° | Sep 1 | 8.5° | |
| Mar 22 | 0.0° | Sep 22 | 0.0° | |
| Apr 1 | 4.2° | Oct 1 | -2.9° | |
| May 1 | 14.8° | Nov 1 | -14.2° | |
| June 1 | 22.0° | Dec 1 | -21.79° | |
| June 22 | 23.4° | Dec 22 | -23.4° |
There are two other important points on the east-west line (x-axis). They are the Bailey Points that indicate time and direction of sunrise or sunset. For example when you stand on a particular date on the walkway and you look toward the west Bailey point, the sight line tells you the time of sunrise. (During summer and fall your dial needs to mark hours before 6am.) Look 180° in the opposite direction from the west Bailey Point and that is the direction of sunrise. Likewise if you look toward the east Bailey point, the sight line tells you the time of sunset. (During summer and fall your dial needs to mark hours after 6pm.) Look 180° in the opposite direction from the east Bailey Point and that is the direction of sunset. To include the Bailey Points on your sundial, they are a distance +/- Bailey from the origin along the east-west (x-axis) line:
\[ \begin{equation} BaileyPoint = \pm M \cos^2(\phi) \sqrt{1-tan^2(\delta)tan^2(\phi)} \end{equation} \]
For the best approximation to the BaileyPoint positions, use \(\delta\) = 20°.
Now that you have the theory of the analemmatic dial, here are two attachments that show step by step the layout of the analemmatic sundial and a spreadsheet with all the mathematics for determining the ellipse shape, location of hour marks, Bailey Points, and the monthly distance marks on the walkway.
