Details

Published: 05 November 2020

Hits: 8891

Alessandro Gunella
Translated by Robert Kellogg

Introduction

We consider here the analemmatic sundial with a gnomon that moves on a calendar line (or zodiac walkway) while remaining perpendicular to the dial plane (though in some designs it can be inclined). If the gnomon is not in the plane of the local meridian, the dial is no longer as simple. From a practical point of view where people cast their shadow to tell time, we shall consider perpendicular gnomons (people as the shadowcasters).

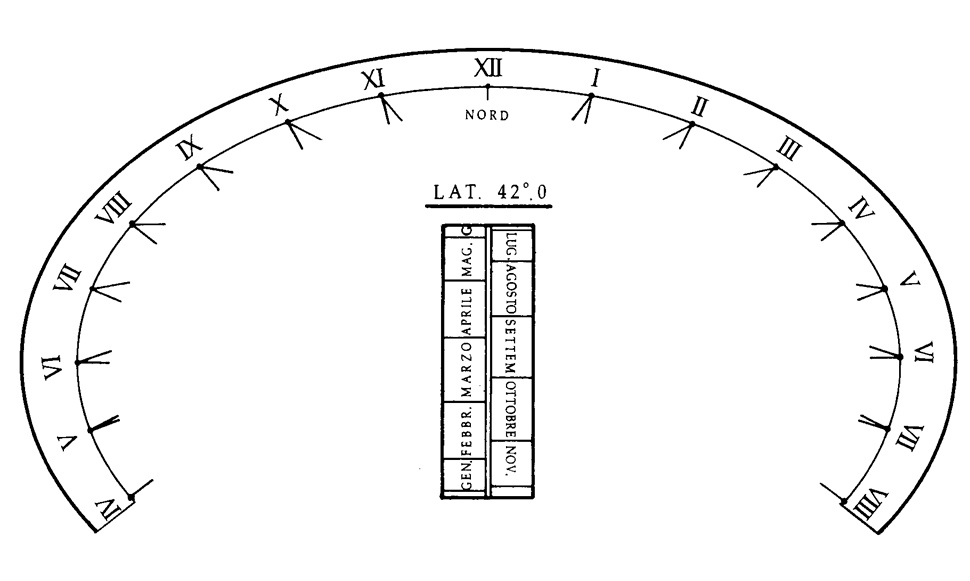The analemmatic sundial has been called by some a "novelty". That is, it lends itself very well to be in-serted as "urban furniture" in public gardens or on a playground. The dial has a rather wide ellipse, stretching in diameter from a handful of meters up to ten meters, drawn appropriately oriented on a nearly horizontal surface. Along the north-south minor axis is the calendar (the zodiac) usually limited to the months of the year. The result can be seen from the illustration (Fig.1): those who want to read the time stand on the corresponding zodiac point for the appropriate date, then the shadow of one’s head points to the hour marks on the ellipse, giving local time. The interest lies precisely in the fact that this is a "human” gnomon" sundial.

We know that the theoretical basis of the Analemmatic Sundial derives from the treatise of Vaulezard (1640), and from that of Foster (1654). From there it evolved through the French treatises of Ozanam and later of Bédos and Lalande. Of interest, the oldest analemmatic sundial known is from the churchyard at Bourg-en-Bresse dating from 1530.

The demonstration of the Analemmatic Sundial’s function is sometimes difficult to understand (for example that of Bédos). Once people understood that the ellipse and zodiac worked as a sundial, they no longer questioned the proof of why it worked. Those who dealt with the problem of showing how the dial worked later tried to enrich the “novelty” with useless drawings, such as the lemniscate of the equal hours, which is notoriously valid only for midday. Very complicated theoretical constructions given by French authors can be cited, who evidently copied from one another, but have never been subjected to criticism. 

An Extremely Simple Interpretation

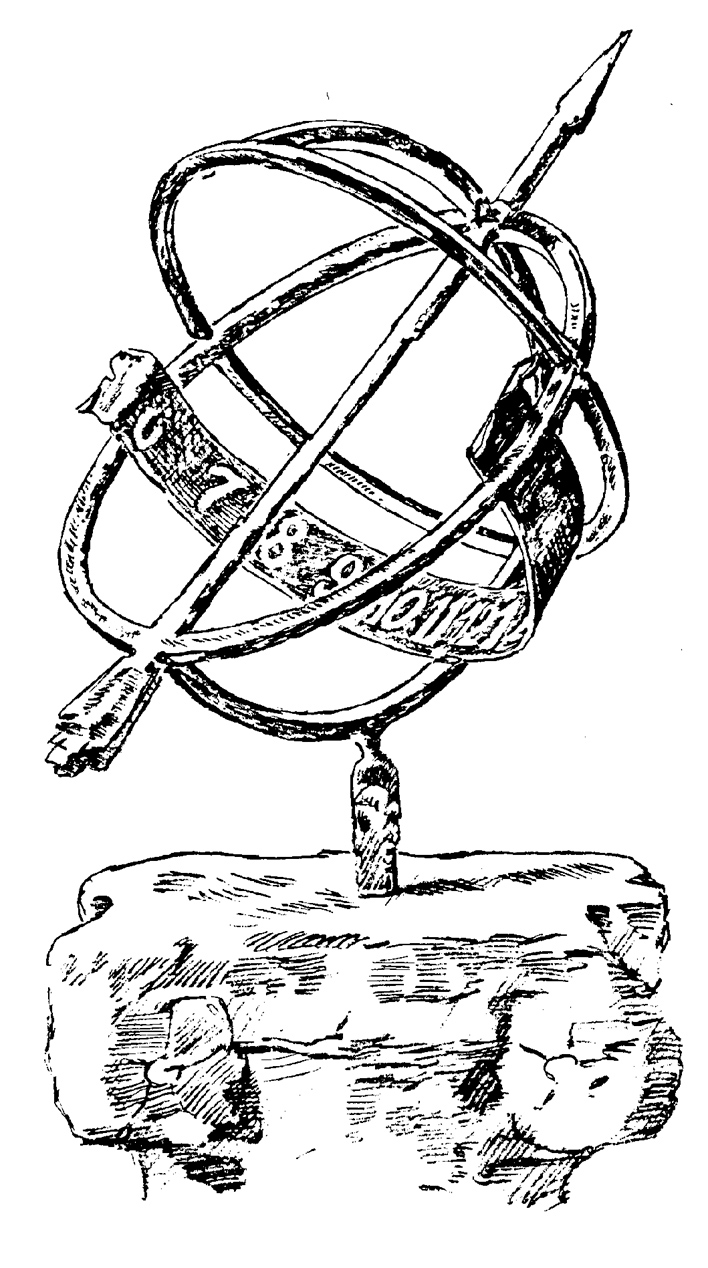I don't pretend to be original and the addage "Nihil sub sole novi" cetainly holds true. The demonstration I propose is based on the armillary sphere sundial (Fig. 2) and is extremely simple, yet I have consulted several books of gnomonics, old and less old, but have never found an equivalent. I apologize to those who see the problem from an exclusively mathematical point of view. I belong to the past and I insist on using graphics.

An Equinoctial Sundial (equatorial sundial) can be easily made using a simplified variant of the armillary sphere and related projections (Fig. 3) We start with a plane view equatorial circle XYZ, of radius R with uniform hour marks from 6am (at Z) to noon (at Y) and continuing to 6pm (at X). A stylus is perpendicular to the equatorial circle at C, represented as a dot in the top portion of Fig 3.

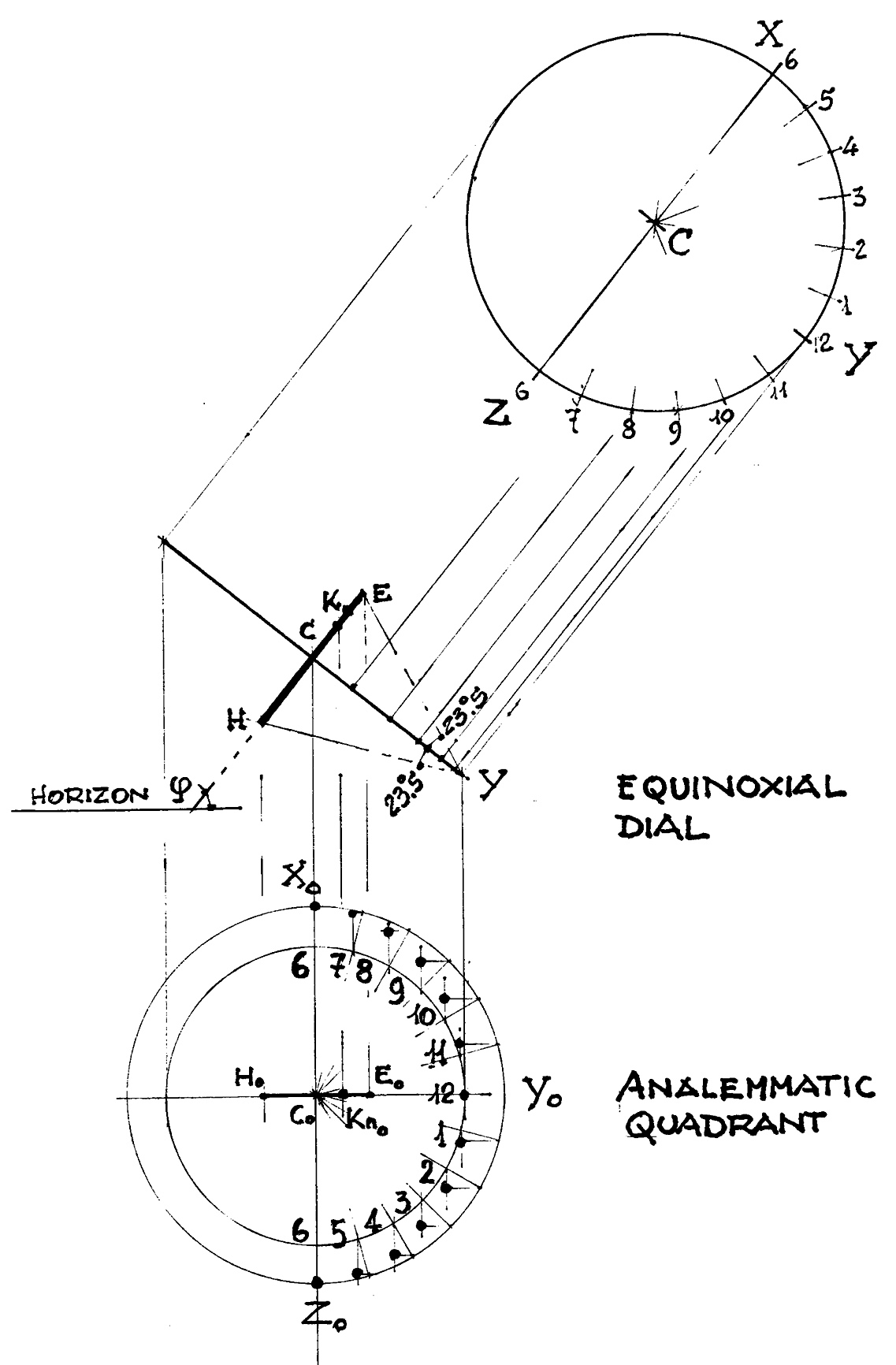Then we view the equatorial circle in a side view with the circle oriented with the earth’s equatorial plan and stylus, now visible as ECH passing through the center C of the circle and oriented to the polar axis of the earth. (middle of Fig. 3) The Equinoctial Dial is now projected onto the horizontal plane. (bottom of Fig. 3) Imagine a plumb line hanging down from each hour mark from the edge of the equatorial circle to the horizontal plane. Those are the “dots” shown from 6am to 6pm.

Rather than drawing the ellipse of the equatorial circle and time marks, we show the semi-minor and semi-major axis circles. The hour marks project an ellipse between the circles.

Again looking at the Equinoctial Dial, the stylus point at C will cast its shadow on the equatorial circle. Consider an hour mark on the equatorial circle’s circumference and a shadow length that just touches this hour mark. At summer solstice the shadow cast will be from point E, and at winter solstice the shadow case will be from point H. Note that from the edge of the equatorial circle (e.g. at point Y) the extreme points CE and CH have an angular change of +/- 23.5 deg

If you choose any point Kn on the EH segment, this represents a position of the solar declination of a given date: Kn = R× tan(sun declination). You can indicate the position Kn spaced every month or even for every day of the year. Thus, if any point Kn is chosen on the stylus segment EH, it will be possible to identify an "almost one-to-one" correspondence between Kn and the date. Of course there will be two days of the year that point Kn projects its shadow length to touch the equatorial circle.

Now imagine a plumb line hanging down from the stylus at point Kn to somewhere on ground plane along meridian north-south line. (Fig. 4)  In fact we can imagine a number of plumb lines hanging down from each of the hour marks to the horizontal dial as well. The plumb line from Kn creates a sort of vertical stylus, valid only for that date. But we know from the Equatnoctial Dial that the shadow of Kn just meets the hour marks. For the projection we see vertical shadow planes ending from the Kn plumb line to each of the hourly plumb lines. These planes will contain all the "solar rays" projecting from the point Kn onto the ellipse of hour points. In other words, the shadow of the plumb line of Kn, passes through the hourly points on the ground projection of the equatorial circle.

On another date the point Kn will change, and there will be a new bundle of vertical line, but the planes projected correctly to the time marks on the ground. Quod demonstrandum erat. (Thus is demonstrated)

I would point out that one of the semi-major axes of the ellipse is the radius of the circle of the equatorial dial, and the other semi-axis is the projection of the radius on the plane of the analemmatic dial and depends on the latitude of the sundial site. The reader may do the math if he/she wishes.

The technique for constructing the ellipse and the time points on it is also quite well known, for example the book by Commandino “de Analemmate” written in 1563. [If you want a thorough reference to Analemmatic Sundials consider purchasing the North American Sundial Society Analemmatic Source Book.]

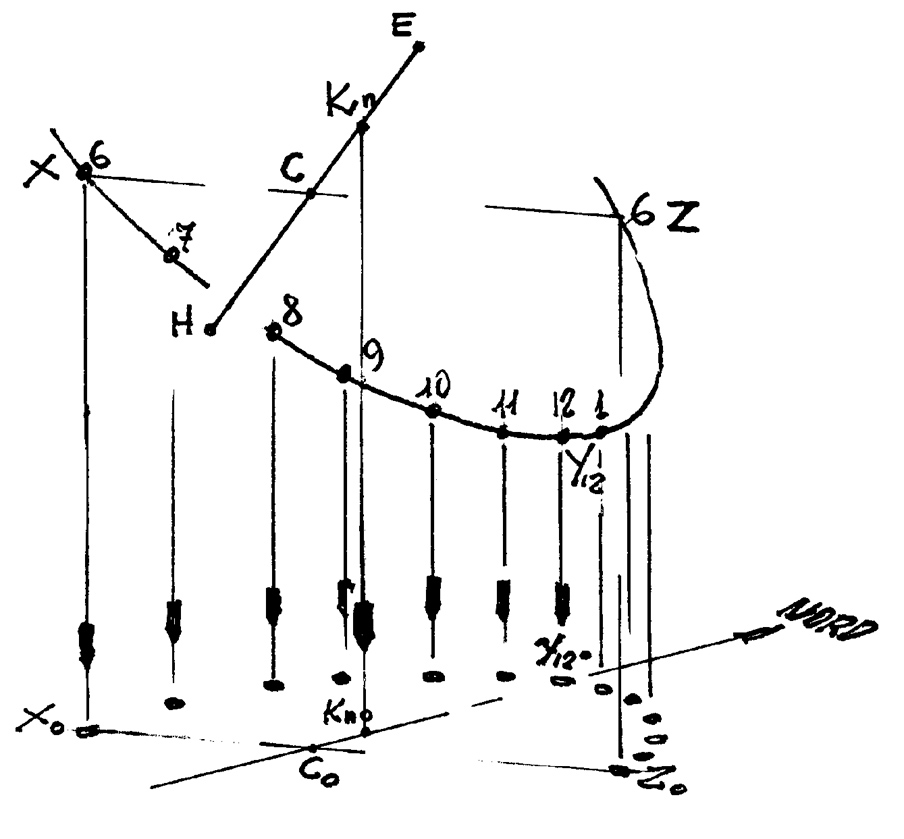In the real world it can also be assumed that the ground plane is not horizontal, but nothing changes in the reasoning: the plumb lines that descend from the time points form a sort of vertical cage of lines which do not depend on the level of the courtyard on which they end. Their figure, like the mutual arrangement of the points Kn relating to the dates, seen in the plan view, is immutable. It is therefore sufficient to mark the ends of both the time mark and Kn plumb lines on this horizontal or inclined plane, making sure that the "mobile stylus" is always vertical [to the true earth]. (The human style, even if the dial is drawn on the side of a hill, will attempt to be vertical to the true earth...at least in intention).

I therefore believe that the tracing of an Analemmatic Sundial on a courtyard, garden, or playground, even when inclined or declining, can take place in a manner similar to those construction workers who trace a new building: they operate on a hypothetical horizontal plane, then transfer their plans with vertical poles and plumb lines onto the irregular ground. (Obviously there is no interest in constructing and analemmatic dial on an unpaved surface.)

It is also possible to broaden the discussion: instead of considering plumb lines, as has been done here, it is possible to create similar projections with variable inclinations using variously horizontal or inclined surfaces. The chosen inclinations are identified by their respective gnomons. The so-called "Foster - Lambert" dial is one of them.

The limiting feature of this research is when the gnomon has a fixed position and is not dependent on the date: the result of course] is the "normal" sundial on any plane with a polar gnomon. But I must repeat that the gnomon (or at least the gnomon point) must always be in the plane of the local meridian.